Parent Functions And Transformations: It is not uncommon to imagine two tasks that love each other, creating a new function when you hear the term parent function. There are more similarities than you might think!
Likewise, family members share similar behavior, genes, characteristics, and each other in the same way we do with our own family; likewise, families of functions share similar algebraic properties, graphs, and behaviors.
Quadratic functions are an example of a family of functions. The highest exponent of quadratic functions is 2, and their graphs are all parabolas, so they share the same shape and particular characteristics.
That’s not precisely true; however, there are some parallels between parents’ and parents’ functions. In mathematics, we have certain groups of functions that are called families of functions. Families of functions have parents as well, just like our own families.
Generic Transformations of Functions
Table of Contents
The “parent functions” assume the simplest form of the function; in other words, the function either goes through the origin (0,0) or if it doesn’t go through the origin, it isn’t shifted. Whenever a function is shifted, compressed, flipped, or stretched from its “parent function,” it is said to be transformed and is a transformation of a function.
T-charts are helpful tools when dealing with function transformations. Let us assume that the quadratic parent function y=x^2 transforms two units to the right and one unit down (only a shift, not a stretch or a flip).
Consequently, we can create the original T-chart and then insert the transformation points outside the original points. To obtain the newly transformed function, we can then plot the “outside” (new) points as follows:
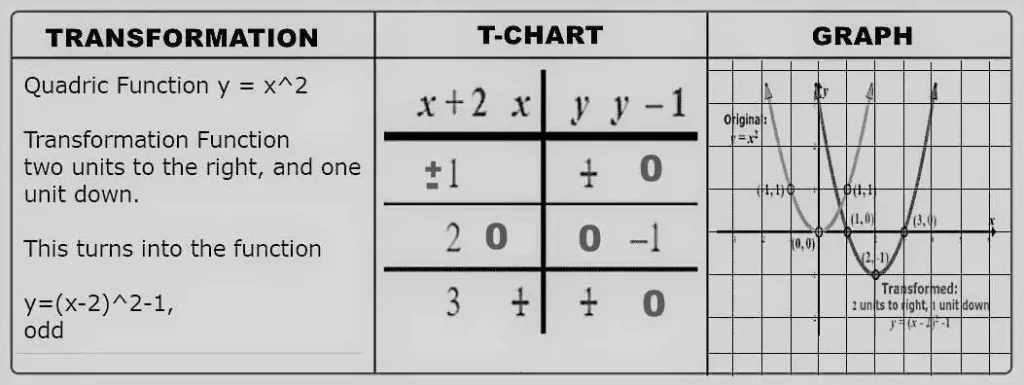
We have to be very careful while looking for the transformation equation. As we have established from the figure when functions are transformed outside of the f(x) part, they are moved up and down, and then you do “regular” math. Some vertical transformations or translations affect the part of the function.
Whenever you transform the f(x) part on the inside, you have to shift the function back and forth (but do the opposite math – because if you isolate the x, you will move everything to the other side). These horizontal transformations or translations affect the x part of the function.
Several methods exist to transform parent functions; I prefer T-charts since they are consistent across functions. Please note that most T-charts include more than just the critical points above to illustrate the graphs better.
We provide essential parent functions for linear, cubic, quadratic, absolute value, rational, and square root functions. You should remember the below points:
- Compatibility with equations.
- Identifies functions by family name.
- Correlates graphs with family names.
- Make sure you match the cards correctly.
- Use this as a matching activity.
- Please do not use it as a flashcard activity.
The following table illustrates the rules for transforming functions. The following sections provide examples and solutions for using the transformation rules.
Recommended: How much does water weigh?
The graph contains the parent function.
This includes essential parent functions for linear, quadratic, rational, cubic, absolute value, and square root functions.
Analyze the graphs and then match them to the equations. Match family names to functions. Match graphs to the family names. Read cards carefully so that you match them correctly.
It is a matching activity. It cannot be used as a flashcard activity.
Here are the rules for transformations:
| TRANSFORMATION RULES FOR FUNCTIONS | ||
| Function Notation | Type of Transformation | Change to Coordinate Points |
| f(x) + d | Vertical Transaction up ”d” units | (x,y) → (x,y+d) |
| f(x) – d | Vertical Transaction down ”d” units | (x,y) → (x,y-d) |
| f(x+c) | Horizontal Transaction left ”c” units | (x,y) → (x-c,y) |
| f(x-c) | Horizontal Transaction right ”c” units | (x,y) → (x+c,y) |
| -f(x) | Reflection over x-axis | (x,y) → (x,-y) |
| f(-x) | Reflection over y-axis | (x,y) → (-x,y) |
| af(x) |
Vertical stretch for |a| >1 |
(x,y) → (x,ay) |
| f(bx) |
Horizontal compression for |b|>1 |
(x,y) → (x/b,y) |
Parent Functions And Transformations Worksheet
We have already discussed that every family function has a parent function. Parent functions are the most straightforward functions that still meet a particular definition of a type of function. If we consider the linear functions that comprise a family of functions, then the parent function would be y = x. It is the most straightforward linear function.
A family of functions can be derived from a parent function by transforming the graph of the parent function. Transformations include horizontal shifting, compressing or stretching horizontally or vertically, reflecting over the x and y axes, and vertical shifting.
The graph illustrates y = 2x*2 + 4x to be the graph of the parent function y = x*2 stretched vertically and shifted left one unit. As a result, the transformations do not affect the general shape of the graph, so every function in a family will have the same appearance and shape.
These transformations are represented mathematically by adding or subtracting terms from the parent function or multiplying by a constant. It can be derived from y = x*2+4x, multiplied by two (constant), and added 4x.
Hope we are able to cover the topic ”Parent Functions And Transformations.” If you still have any doubts or suggestions, write in the comment section given below.

